Direct Instruction: Problem-solving Strategies
Overview
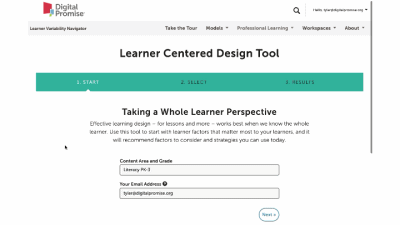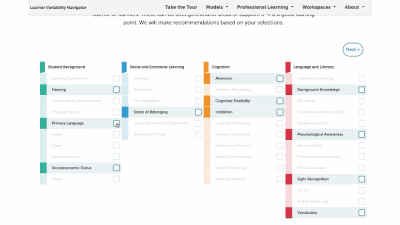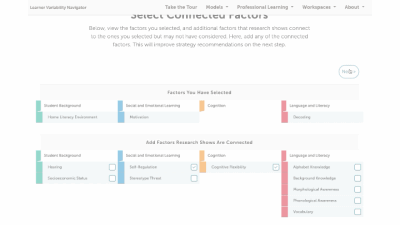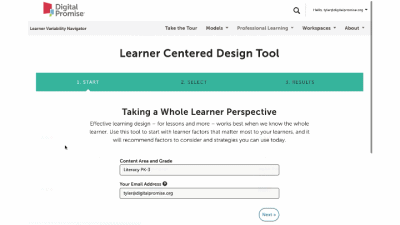
Discussing strategies for solving mathematics problems after initially letting students attempt to problem solve on their own helps them understand how to organize their mathematical thinking and intentionally tackle problems. For students to solve math problems accurately and efficiently, they must learn and compare multiple strategies, articulate why they chose one strategy over another, and flexibly apply them. However, research shows that students develop deeper conceptual understanding and Mathematical Flexibility when they engage in problem-solving and productive failure before direct instruction.
Example: Use This Strategy In in the Classroom
Design It into Your Product
Videos are chosen as examples of strategies in action. These choices are not endorsements of the products or evidence of use of research to develop the feature.
Learn how DreamBox Learning allows students to solve problems in multiple ways. By explicitly promoting problem solving with different strategies, this product builds Mathematical Flexibility, while also developing conceptual math understanding.
Additional Resources
Additional examples, research, and professional development. These resources are possible representations of this strategy, not endorsements.
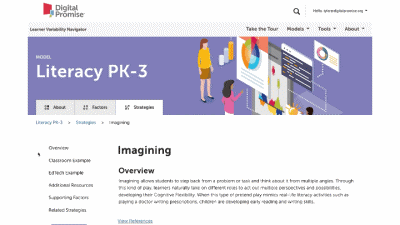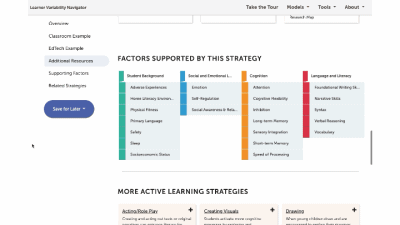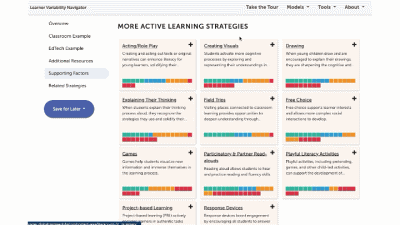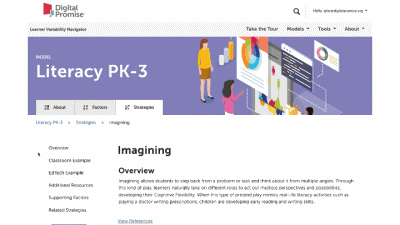
Factors Supported by this Strategy
More Instructional Approaches Strategies
CRA is a sequential instructional approach during which students move from working with concrete materials to creating representational drawings to using abstract symbols.
Knowing the language of math is critical because students must use this language to understand math concepts and determine calculations needed.
In explicit number naming, the structure of the number name labels the number in Place Value order and clearly states the quantity.
Thinking of and about patterns encourages learners to look for and understand the rules and relationships that are critical components of mathematical reasoning.
Teaching students to recognize common problem structures helps them transfer solution methods from familiar to unfamiliar problems.
In guided inquiry, teachers help students use their own language for constructing knowledge by active listening and questioning.
Math centers with math games, manipulatives, and activities support learner interests and promote the development of more complex math skills and social interactions.
Through short but regular mindfulness activities, students develop their awareness and ability to focus.
Instruction in multiple formats allows students to activate different cognitive skills to understand and remember the steps they are to take in their math work.
Using multiple methods of assessment can help educators gain a comprehensive understanding of learner progress across a wide range of skills and content.
A parent evening meeting about how to support numeracy at home with one follow-up meeting with each family has shown strong results for students' math development.
When teachers connect math to the students' world, students see how math is relevant and applicable to their daily lives.
A strengths-based approach is one where educators intentionally identify, communicate, and harness students' assets, across many aspects of the whole child, in order to empower them to flourish.
Three-phase lesson format is a problem-solving structure to promote meaningful math learning by activating prior knowledge, letting students explore mathematical thinking, and promoting a math community of learners.
Untimed tests provide students the opportunity to flexibly and productively work with numbers, further developing their problem-solving abilities.